题目分析

想求解这个题目难度很小，找到规律就可以轻松的解答。但是能否按照说明中的要求，在$O(1)$的空间复杂度只内求解呢？

找规律

我们首先介绍最简单的方法，**前面k个数字就是原来最后的k个数字，即newNums[i] = nums[n - k + i]，其他的所有数字都会往后移动k个位置，即newNums[i] = nums[i - k]**。

获得新的newNums[i]就是最终的答案，因为我们没有返回值，需要在原数组修改，我们重新赋值一次即可。

要注意的是k可能很大，因为移动n次相当于没有移动，要对n求模。

算法的**时间复杂度为$O(n)$，空间复杂度为$O(n)$**，其中n是数组中元素的个数。

#include<iostream>
#include<vector>
#include<algorithm>

using namespace std;

class Solution {
public:
    void rotate(vector<int>& nums, int k) {
        int lens = nums.size();
        k %= lens;
        vector<int> newNums(lens);
        for (int i = 0; i < lens; i++) {
            newNums[i] = i < k ? nums[lens - k + i] : nums[i - k];
        }
        copy(newNums.begin(), newNums.end(), nums.begin());
    }
};

模拟

模拟的思路是来自于数据结构，题目的要求类似于一个队列操作，每次从队尾取出元素，在队头插入元素。因此一个简单的做法是将元素都放入一个队列，然后移动k次即可。

将元素移动到队列所用的时间是$O(n)$，因此算法的**时间复杂度为$O(n)$，空间复杂度为$O(n)$**，其中n是数组中元素的个数。

当然小伙伴们也可以在数组中进行尾部删除和头部插入，不借助队列，这样**时间复杂度为$O(n^2)$，空间复杂度为$O(1)$**。

#include<iostream>
#include<vector>
#include<deque>

using namespace std;

class Solution {
public:
    void rotate(vector<int>& nums, int k) {
        int lens = nums.size();
        k %= lens;
        deque<int> newNums(lens);
        for (int i = 0; i < lens; i++) {
            newNums[i] = nums[i];
        }
        while (k--) {
            int x = newNums.back();
            newNums.pop_back();
            newNums.push_front(x);
        }
        for (int i = 0; i < lens; i++) {
            nums[i] = newNums[i];
        }
    }
};

环状替换

这个方法是我参考Leetcode官方题解中的一个方法。我们的问题在于如果将第一个元素放到第1+k个元素中，这时如果考虑第二个元素就会导致第1+k个元素已经被覆盖，当考虑到第1+k的元素就会发生错误。因此我们可以将第一个元素放到第1+k个元素时，考虑第1+k个元素应该放在1+2k处。然后考虑第1+2k个元素应该放在1+3k处。。。

用样例进行举例[1,2,3,4,5,6,7]，k=3。这时我们考虑1，移动3个单位后，1应该放在4这个位置，那么我们将4拿起来，将1放在该位置上。然后我们考虑4，4应该放在7这个位置上，那么我们将7拿起来，将4放在该位置上。然后我们考虑7，7应该放在3这个位置上，那么我们将3拿起来，将7放在该位置上。。。最后可以得到正确的结果。

但是这个问题的难点是当某些情况，我们如何知道后面的数字是否需要移动了呢？
可能这种说法难以理解，仍然举一个例子[1,2,3,4,5,6]，k=2，1放在3，3放在5，5放在1形成了一个闭环。这时就应该停止了。然后2放在4，4放在6，6放在2，也形成了一个闭环。那么我们是否还要分析3呢？答案是不需要的，如何判断3不需要是这个问题的难点。

其中一个思路是设置一个计数器cnt，进行一次放置操作，cnt++，当cnt等于n时，说明这n个数都已经安排过了，因此可以停下。

还有一个思路是数学思路，形成闭环数组一定是遍历了整数圈，不妨记为a，在本例中135是一个闭环，数组遍历了1圈。放置了b个数字，这里是3个数字。其中k=2。一定满足an = bk这个规律，这时显而易见的。因为一旦形成闭环，从i开始的放置操作就结束了。因此我们要让a最小，因为an一定是n的整数倍，也要一定是k的整数倍，我们如果证明n和k的最小公倍数满足等式，说明这时a一定是最小的。不妨设n和k的最小公倍数为m，m = pn，m = qk，那么p等于a，q = b，都是整数，满足公式，因此an = bk = n和k的最小公倍数lcm(n, k)。这时b = lcm(n, k) / k。说明一次遍历会放置b个元素，那么访问到所有的元素需要访问n / b次。根据数学概念nk / lcm(n, k) = gcd(n, k)其中gcd为最大公约数。

上面的分析有一些复杂，但是也比较好理解，小伙伴们用[1,2,3,4,5,6]这个样例，分别让k=2，k=3，k=4，k=5在草稿纸上面模拟一个这个过程就容易理解了。k=2时遍历1和2两个数字，遍历每个数字放置3次。k=3时，遍历1，2和3三个数字，遍历每个数字放置2次。k=4时，遍历1和2两个数字，每个数字放置3次。k=5时，遍历1这个数字，这个数字放置6次。

算法的**时间复杂度为$O(n)$，空间复杂度为$O(1)$**，其中n是数组中元素的个数。

#include<iostream>
#include<vector>
#include<algorithm>

using namespace std;

class Solution {
public:
    int gcd(int a, int b) {
        return a == 0 ? b : gcd(b % a, a);
    }

    void rotate(vector<int>& nums, int k) {
        int lens = nums.size();
        k %= lens;
        int n = gcd(k, lens);
        for (int i = 0; i < n; i++) {
            int nextIdx = (i + k) % lens, curVal = nums[i];
            while (nextIdx != i) {
                swap(curVal, nums[nextIdx]);
                nextIdx = (nextIdx + k) % lens;
                curVal = curVal;
            }
            nums[nextIdx] = curVal;
        }
    }
};

优化找规律

这个题目的最优解法类似一个脑筋急转弯。我们想最后面的k个元素要放到最前面。我们并且要保持相对顺序。

那么我们先不管相对顺序，我们如何将后面k个元素放到最前面k个元素。是不是逆序即可。

逆序后，最后面k个元素在最前面，最前面的n-k个元素在最后面。但是这时候前面k个元素的顺序也是逆序的，并没有保持相对顺序，后面n - k个元素的顺序也是逆序的，也没有保持相对顺序，这时我们单独逆序前面k个元素和后面n - k个元素即可。

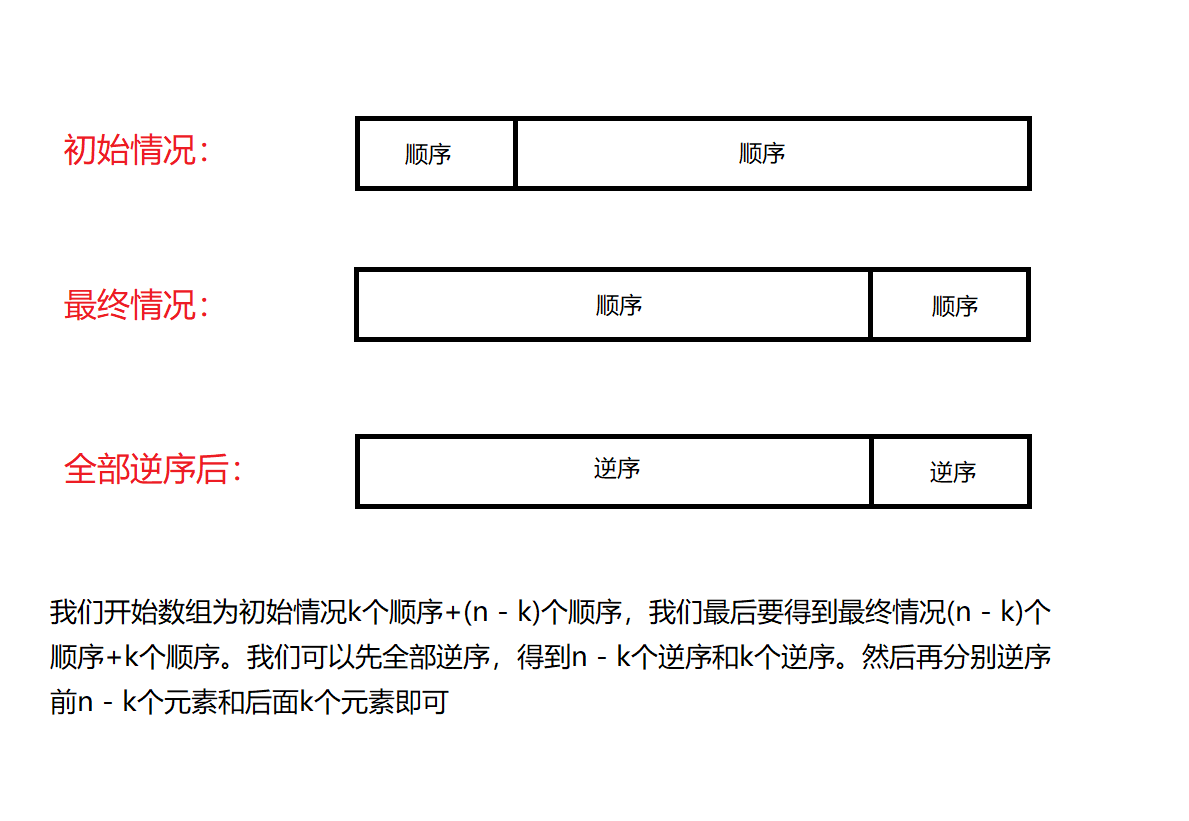
算法的**时间复杂度为$O(n)$，空间复杂度为$O(1)$**，其中n是数组中元素的个数。

#include<iostream>
#include<vector>
#include<algorithm>

using namespace std;

class Solution {
public:
    void rotate(vector<int>& nums, int k) {
        k %= nums.size();
        reverse(nums.begin(), nums.end());
        reverse(nums.begin(), nums.begin() + k);
        reverse(nums.begin() + k, nums.end());
    }
};

刷题总结

这个题目也是比较经典的题目了，这几种方法都非常好，希望小伙伴们都能够掌握。